Анализ сетевого графика

Понятие критического пути

Разбиение проекта на множество работ и определение связей между работами во времени - задача весьма трудоемкая. Ее решение помогает выявлению промежуточных целей и направления действий, которым должен следовать руководитель. Это дает возможность решить, какие работы должны быть выполнены для осуществления различных подпроектов, позволяет правильно распределить все работы. После построения сетевой модели ход действий становится ясным и можно приступить к выполнению проекта; другими словами, сетевое планирование предусматривает выработку некоторой стратегии действий.

При решении задачи планирования может быть извлечена дополнительная информация из сетевой модели самого плана. Это приводит нас к стадии анализа, в котором такие понятия, как критический путь и резерв времени работы, играют ключевую роль.

Критический путь

. Первый шаг в анализе графа работ заключается в нахождении критического пути

(или путей) сети. Для определения этого понятия мы рассмотрим простейшую сеть, изображенную на рис. 9.5.

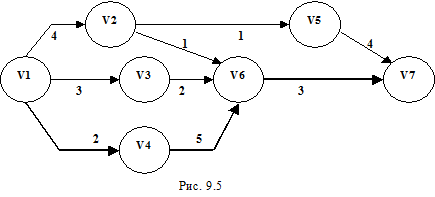
Замечания.

В наших примерах мы не будем обсуждать реального смысла работ, как это делалось в предыдущих примерах и упражнениях. Как правило, вся символика будет той же, что на рис. 9.5. Символом V

(вершина) обозначаются события; пара (V

i, V

j) определяет работу a

ij; число, стоящее около каждой стрелки, означает время выполнения соответствующей работы.

В сети на рис. 9.5 V

1 означает начало проекта, а V

7 - его окончание. Заметим, что от вершины V

1 к вершине V

7 можно пройти по сети четырьмя различными путями; для каждого пути мы можем определить его временную продолжительность - длину пути, т.е. сумму продолжительностей последовательных работ, образующих путь. Пути и их продолжительности будут следующими.

Путь Продолжительность

V

1 - V

2 - V

5 - V

7 4 + 1 + 4 = 9

V

1 - V

2 - V

6 - V

7 4 + 1 + 3 = 8

V

1 - V

3 - V

6 - V

7 3 + 2 + 3 = 8

V

1 - V

4 - V

6 - V

7 2 + 5 + 3 = 10

Определения:

1. Максимальное значение в множестве продолжительностей всех путей (оно может достигаться на нескольких путях) называется полным временем осуществления проекта

. Это значение определяет наикратчайшее время, за которое может быть выполнен весь проект.

2. Любой путь, длина которого равна полному времени осуществления проекта, называется критическим путем

.

В приведенном примере максимальная продолжительность пути равна 10 единицам. Невозможно закончить все работы сети до истечения 10 единиц времени, если отчет начинается со времени совершения события V

1. Отсюда следует, что полным временем осуществления проекта будет 10 единиц, а критическим путем V

1-V

4-V

6-V

7.

Чтобы уменьшить полное время осуществления проекта, необходимо сократить продолжительность работ, лежащих на критическом пути. Уменьшение продолжительности работы, не принадлежащей критическому пути, не отразится на изменении полного времени осуществления проекта.

Методы определения критического пути

Нахождение критического пути может быть выполнено с помощью методов, требующих информации, которая используется на последующих стадиях анализа. Эти методы легко применимы при счете вручную, и могут быть запрограммированы для компьютера. На практике для большой сетевой модели, тем более, если анализ должен повторяться через определенные интервалы времени, применение компьютерной программы значительно упрощает задачу.

Процедура отыскания критического пути состоит в следующем. Прежде всего, составляется список всех событий в той последовательности, в которой они должны выполняться, т.е. по сети слева направо. Затем для каждого события вычисляются так называемые ранний срок (E

) и поздний срок (L

) свершения события. Если отыскание критического пути выполняется вручную, то эти значения можно записать сразу на графике. Тогда любой путь, такой, что для всех событий, входящих в него, E = L

, будет одним из возможных критических путей.